Introduction

I’ve been using gnuradio with my SDR device for a while now. While it’s a really neat tool, there’s nothing like implementing something yourself in code to fully understand what’s going on under the hood, so I wrote this FM broadcast receiver in C.

Implementation

Design & Testing

First, I came up with a design and tested it in gnuradio to make sure it would work before implementing it in code. Each of these blocks has a corresponding C implementation that I will discuss below.

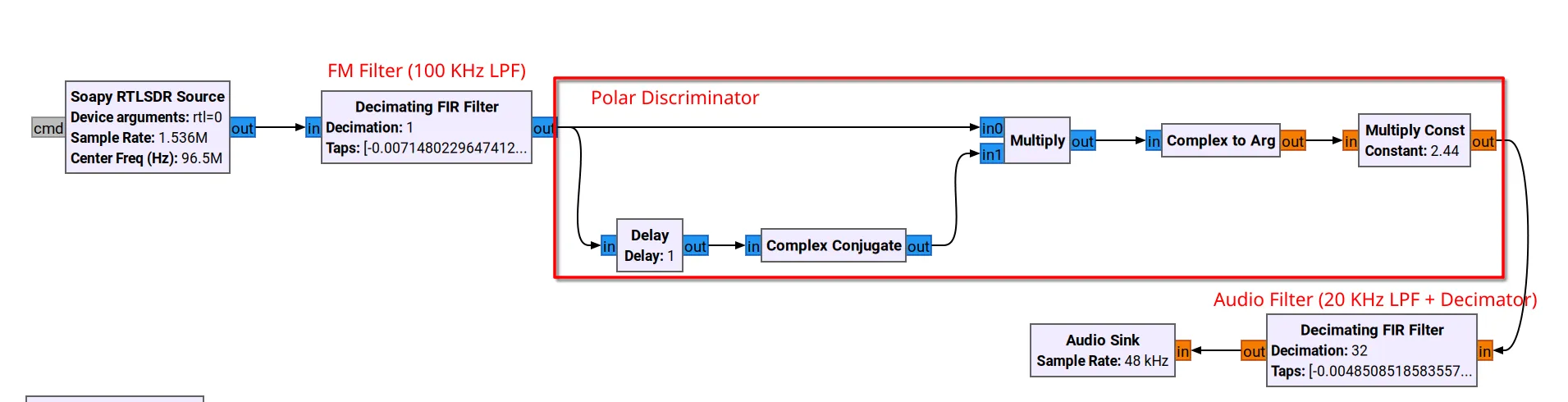FM Demodulator tested in gnuradio

Sampling

Sampling is done using librtlsdr. Setup is very simple: just give it the sampling rate and center frequency, and it does the rest. An extra scaling step from the default 0-255 range to -1.0 to 1.0 range was required for these samples to be useful with the demodulation method I chose.

// Read SDR_BUFFER_SIZE samples range 0-255 from SDR device
void read_samples() {
    int n_read;
    rtlsdr_read_sync(dev, raw_signal, 2 * SDR_BUFFER_SIZE, &n_read);
}

// Scale IQ samples to range -1.0 to 1.0
void scale() {
    for(int i = 0;i < 2 * SDR_BUFFER_SIZE;i++) {
        scaled_signal[i] = ((double)raw_signal[i] - 127.5) / 127.5;
    }
}

Polar Discriminator

As you might imagine, recovering information from a frequency-modulated signal requires estimating the incoming signal’s frequency. Since my SDR device provides IQ samples, I chose to use a Polar Discriminator for this purpose. It works by exploting the fact that the product of a complex number by the conjugate of another complex number has a phase equal to the difference in phases of the numbers being multiplied. Since frequency is essentially the derivative of phase, and since the time between samples is short, this phase difference is a good estimate of instantaneous frequency.

anejθn(an−1ejθn−1)∗=anejθn⋅an−1e−jθn−1=anan−1ej(θn−θn−1)a_ne^{j\theta_n}(a_{n-1}e^{j\theta_{n-1}})^* = a_ne^{j\theta_n} \cdot a_{n-1}e^{-j\theta_{n-1}} = a_na_{n-1}e^{j(\theta_n-\theta_{n-1})}

Then to convert this phase difference to the modulating signal’s original frequency in Hertz:

fm=(θn−θn−1Tsradianssecond)(1 cycle2π radians)=(θn−θn−1)Fs2πf_m = (\frac{\theta_n-\theta_{n-1}}{T_s}\frac{\text{radians}}{\text{second}})(\frac{1\text{ cycle}}{2\pi\text{ radians}}) = (\theta_n-\theta_{n-1})\frac{F_s}{2\pi}

Per Wikipedia, the baseband signal will have the following form:

fΔfmsin(2πfmt)\frac{f_\Delta}{f_m} sin(2\pi f_mt)

So multiply by fmfΔ=Fs2πfΔ\frac{f_m}{f_\Delta} = \frac{F_s}{2\pi f_\Delta} to normalize the amplitude of the estimated signal

Here’s what the code for this ended up looking like

double previous_sample_i = 0, previous_sample_q = 0;
void polar_interpolator() {
    for(int i = 0;i < 2 * SDR_BUFFER_SIZE;i+=2){
        double current_sample_i = fm_filter_output[i];
        double current_sample_q = fm_filter_output[i + 1];

        // Conjugate
        previous_sample_q *= -1.0;

        // Estimate phase difference
        double real = current_sample_i * previous_sample_i - current_sample_q * previous_sample_q;
        double imag = current_sample_i * previous_sample_q + current_sample_q * previous_sample_i;
        double arg = atan2f(imag, real);

        // Update
        previous_sample_i = current_sample_i;
        previous_sample_q = current_sample_q;
        polar_discriminator_output[i / 2] = arg * (1.0 * SDR_SAMPLE_RATE / (2.0 * M_PI * FM_DEVIATION));
    }
}

Filtering

I used T-Filter to generate linear-phase FIR filter coefficients. The actual filtering process was implemented as a direct convolution:

y[n]=∑k=−∞∞f[n−k]h[k]y[n] = \sum_{k=-\infty}^{\infty}f[n-k]h[k]

After accounting for the fact that the filters are causal and finite length, the code implementation looked like this:

for(int n = 0;n < output_length;n++) {
        int h_idx = 0, x_idx = n;
        double acc = 0;
        while(x_idx >= 0 && h_idx < AUDIO_FILTER_LENGTH) {
            if(x_idx < SDR_BUFFER_SIZE) {
             acc += polar_discriminator_output[x_idx] * audio_filter_coefficients[h_idx];
            }
            x_idx--;
            h_idx++;
        }

but there was an issue.

Overlap Add

When processing data in real-time, it’s necessary to process it in chunks. In my program, I’m reading 32768 samples at a time, and my FM filter’s impulse response is 157 samples long. The linear convolution of these two will be 32768 + 157 - 1 = 32924 samples long. What do I do with the extra 156 samples? Initially, I just discarded them and only sent the first 32768 to the speaker. This actually worked pretty well, but often there would be an audible crackle behind the music. To remediate this, I implemented the overlap-add method. Here’s how it works :

Suppose you’re processing L samples at a time and your filter length is P. The output of the convolution will be L + P - 1 samples long. Take the first L samples of the result and output them as usual. Store the remaining P - 1 output samples in another buffer. These correspond to future outputs that you haven’t sent to the speakers yet. In the future, when you get the next L samples, add the first P - 1 output samples to the P - 1 samples you stored in the previous round to get the total and correct output for that time range.

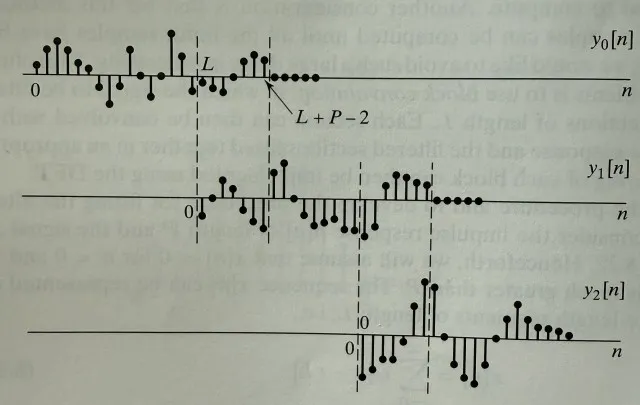Overlap-add diagram (Oppenheim, Schafer 1999)

Final code for the audio filter below. I’ve omitted the FM filter since it’s the same thing but longer because it works on complex instead of real samples.

double audio_filter_tail[AUDIO_FILTER_LENGTH - 1] = {};
void audio_filter() {
    if(!use_audio_filter) {
        for(int i = 0;i < SDR_BUFFER_SIZE;i++) {
            audio_filter_output[i] = polar_discriminator_output[i];
        }
        return;
    }
    uint32_t output_length = SDR_BUFFER_SIZE + AUDIO_FILTER_LENGTH - 1;
    for(int n = 0;n < output_length;n++) {
        int h_idx = 0, x_idx = n;
        double acc = 0;
        while(x_idx >= 0 && h_idx < AUDIO_FILTER_LENGTH) {
            if(x_idx < SDR_BUFFER_SIZE) {
             acc += polar_discriminator_output[x_idx] * audio_filter_coefficients[h_idx];
            }
            x_idx--;
            h_idx++;
        }
        if(n < AUDIO_FILTER_LENGTH - 1 && use_overlap_add) {
            audio_filter_output[n] = acc + audio_filter_tail[n];
        }
        else if(n < SDR_BUFFER_SIZE){
            audio_filter_output[n] = acc;
        }
        else {
            audio_filter_tail[n - SDR_BUFFER_SIZE] = acc;
        }
    }
}

Audio output

I used nanoalsa to play my final audio samples. It’s very easy to setup and get going. One issue I ran into regarding sound output was that I had to constantly send samples to the sound card or I’d start getting buffer underrun errors or weird audio effects. With a single thread, the time to collect and process new samples was too long to keep the sound card buffer full. Here’s the approach I took to resolve this

  1. Thread A begins sampling. When it’s finished, signal thread B and begin processing
  2. Thread B begins sampling. When it’s finished, signal thread A and begin processing
  3. Thread C constantly outputs whatever’s in the audio_output buffer to the sound card

This approach ensures that there’s always new sound data available and that samples are constantly being collected and processed.

Sequence Diagram

Final Result

In the end, I had a console program that lets you tune different stations as well as enable/disable the different filters and overlap-add method to easily hear what impact each piece has on the output. If you’re interested, the full source code is available on Github